-측정값들과 제일 가까운 직선을 그리는 방법
-값을 정확하게 측정할 수 없는 경우에 유용하게 사용

공식

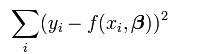
• 위 공식이 최소가 되도록 하는 함수 f(x)를 구하는 것이 최소제곱법의 원리

원리

• 위의 그림에서 각 데이터 좌표에서 최적 함수까지의 거리
  • 직선이 최적의 함수라면, 이 차이가 가능한 한 최소의 값을 가질 것이다
  • 최소제곱법은 이 편차의 제곱을 최소화하기 위한 방법
    • 이 편차를 그대로 더하면 양의 값과 음의 값의 합이 되기 때문에 적합한 결과를 얻지 못한다
    • 절대값을 사용할 경우, 미분계수 계산 시 문제가 발생할 수 있다
• 데이터가 선형적인 관계라면, f(x)는 보통 y = a + bx 로 표현 가능

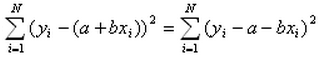
참고

• https://en.wikipedia.org/wiki/Least_squares
• http://bongoras.tistory.com/446
• http://phylab.yonsei.ac.kr/board.aphp?board=excel&indexorder=2&command=body&no=17