-제약이 있는 최적화 문제를 푸는 방법
-어떤 함수가 주어진 제약식을 만족시키면서, 그 함수가 갖는 최대값 혹은 최소값을 찾고자할 때 사용

공식

• L(x,λ) = F(x) + λ*h(x)
  • 변수들에 대해 각각 편미분을 한 식이 0이 되는 값을 구한다
  • 기울기가 같아지는 공통접선을 구하는 것
  • F(x) = F(X)에서 양변에 0에 해당하는 제약식(0 = h(x))을 더해서 F(x) + 0 = F(x) + h(x) 으로 놓고 문제를 푼 것

증명

• z = f(x, y)의 최대값과 최소값을 구하기 위해서는 극값과 경계선에서의 함수 값들을 비교하면 된다
  • D = {(x, y} │ 0 <= x <= 1, 0 <= y < 1}
    • 경계선은 x=0, x=1, y=0, y=1 이므로 경계선에서의 최대값, 최소값을 구할 수 있다
• 만약 아래와 같은 식에서 최대값, 최소값을 구해야 한다면 ?
  
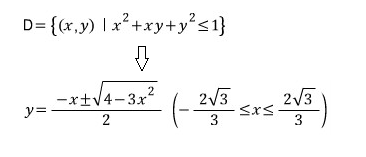
  • 위 식에서 최대값, 최소값을 구하려면 다소 복잡하다
• 경계선에서의 최대값과 최소값을 쉽게 구할 수 있는 방법은 ?
  

예제

• 경계선이 다음과 같이 주어져 있다. f(x, y) = x의 g(x, y) = 0 위에서의 최대값과 최소값은 ?
  
  
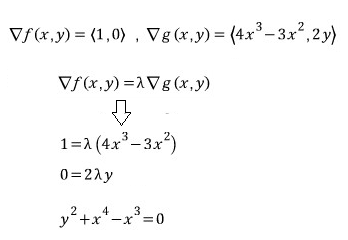
• 이 연립 방정식을 풀게 되면 x=1, y=0, λ=1이 나온다
• f(x, y)는 (1, 0)dptj 최대 혹은 최소값을 갖고 그 값은 f(1, 0) = 1 이다.
  
• 그런데! 임의의 실수 y에 대해 아래와 같은 성질을 만족
• f(x, y) = x는 (0, 0)에서 최소값 0을 갖는다
  
  
• (0, 0)이 라그랑주 승수법에서 나오지 않는 이유는 ?
  • g(x, y)를 좌표평면에 그래프를 그리면 (0, 0)에서 뾰족점을 갖기 때문에 (0, 0)에서 접선을 가지 않기 때문이다

참고

• http://economia.tistory.com/2
• http://zetablog.tistory.com/8
• http://newsight.tistory.com/96
• http://blog.naver.com/mindo1103/90154212128