-두 확률 변수의 사전 확률과 사후 확률 사이의 관계를 나타내는 정리
-P(A│B)를 알고 있을때 P(B│A)를 구할 수 있다

공식

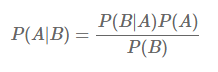
• P(A)는 사건 A가 일어날 확률
• P(B)는 사건 B가 일어날 확률
• P(A │ B)는 사건 A가 일어났을 때 사건 B가 일어날 확률
• P(B │ A)는 사건 B가 일어났을 때 사건 A가 일어날 확률

증명

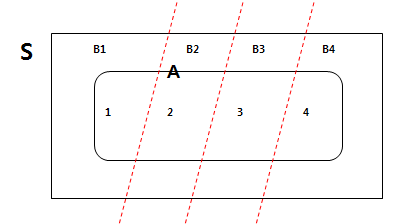
• 표본공간 B1,B2,B3,B4가 상호베타적이며 완비적인 사상들로 분할 되어 있다
• 사상 A와 사상B는 교집합을 형성한다
• 사상 A가 일어날 확률
  • P(A) = P(A ∩ B1) + P(A ∩ B2) + P(A ∩ B3) + P(A ∩ B4)
  • P(A) = P(1) + P(2) + P(3) + P(4)
  • P(A) = P(B1)P(A │ B1) + P(B2)P(A │ B2) + P(B3)P(A │ B3) + P(B4)P(A │ B4)
• B¡의 사전적 확률 P(B¡)와 P(A │ B¡)가 주어진 경우 B¡의 사후적 확률 P(B¡ │ A)를 구한다

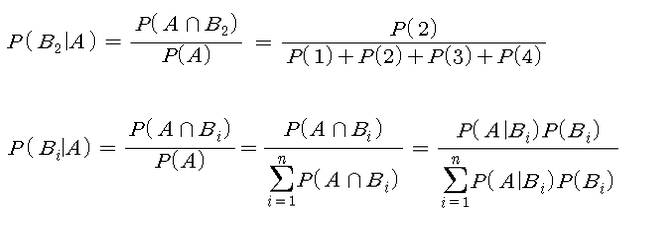
참고

• https://en.wikipedia.org/wiki/Bayes’_theorem
• http://blog.naver.com/lucifer246/188508160