Regression ?

• 두 변수 x와 y와의 관계에 적합한 선
• Regression이 직선인 경우에는 Regression Line(회귀 직선)이라 한다
  

Linear Regression

-머신러닝뿐만 아니라 통계학에서도 다루는 가장 기본적인 알고리즘
-하나의 입력 값(독립 변수)을 가지고 출력 값(종속 변수)을 예측하고 싶을 때 사용

• 장점
  • 구현이 쉽다
  • 타 알고리즘이 비해 수행 속도도 빠르다
  • 많은 분야에 적용하여 사용 가능 하다
• 단점
  • 실세계의 데이터들을 Linear Regression 모델에 적합하게 맞추기 쉽지 않다

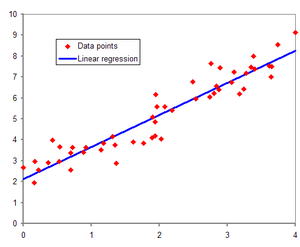
Hypothesis Function

• 최적의 선을 그리는 θ0과 θ1 찾기위해 최소 제곱법, Gradient Descent 등을 수행한다
  • 최적의 선이란 각각의 포인트(훈련 데이터)에서 선까지의 거리의 제곱의 합이 가장 작아 지는 선을 의미
  • 아래 그림에서 빨간 선들의 길이의 제곱의 합이 가장 작아지는 선을 찾아야 한다

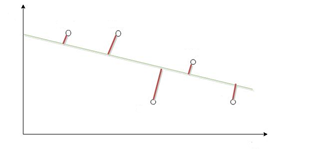
• Training Data의 입력 값 x에 대해 예측된 값 h(x)와 Training Data의 출력 값 y의 차이가 가장 작은 θ0과 θ1을 찾아야 한다

• 직선과 각 포인트의 거리에 대한 합을 구하는 공식은 아래와 같다 (최소 제곱법을 이용)
  • Cost Function라고 부른다
  • 각 차이에 대해 제곱을 한 이유에 대해서는 최소제곱법 참조
  • m은 Training Data의 개수
  • m개의 대한 평균과 미분 계산을 쉽게 하기 위해 2m으로 나눴다
• Cost Function을 계산하기 위해서는 θ0과 θ1 값이 필요
  • θ0과 θ1을 구하기 위해서는 Gradient Descent기법을 사용
  • θ0과 θ1은 동시에 업데이트하여 적용해야 한다
    
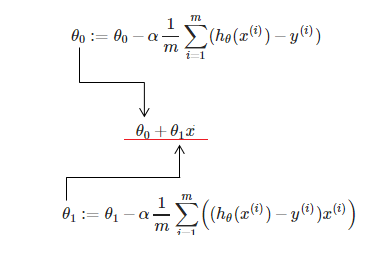
• 최적의 θ0과 θ1을 찾아 h(x) Hypothesis Function을 완성 할 수 있다

참고

• https://www.coursera.org/learn/machine-learning/supplement/Mc0tF/linear-regression-with-one-variable
• http://deepcumen.com/2015/04/linear-regression-2/
• http://www.ftpress.com/articles/article.aspx?p=2248639&seqNum=5