DataStructure

AVL Treeby Pigbrain

-Adelson-Velskii, Landis에 의해 제안된 트리
-Binary Search Tree(BST)에서 Balance가 추가된 트리

BST

  • 장점
    • 탐색속도가 빠르다
  • 단점
    • 편향 트리일 경우 연결리스트와 같은 탐색 속도를 낸다

AVL

  • 탐색 속도는 BST와 동일하다
    • O(log₂n)
  • 노드의 왼쪽 서브 트리와 오른쪽 서브 트리의 높이 차는 ±1이하여야 한다
  • 삽입과 삭제를 할 때 트리의 높이차가 ±2 이상이 되면 회전을 통하여 ±1이하로 만든다
    • 삽입 종류
      • LL 타입 : 왼쪽 서브 트리의 왼쪽 서브 트리에 삽입한다
      • LR 타입 : 왼쪽 서브 트리의 오른쪽 서브 트리에 삽입한다
      • RR 타입 : 오른쪽 서브 트리의 오른쪽 서브 트리에 삽입한다
      • RL 타입 : 오른쪽 서브 트리의 왼쪽 서브 트리에 삽입한다
    • 회전 종류
      • LL 회전 : 오른쪽으로 회전시킨다
      • LR 회전 : 왼쪽으로 회전시킨 후 오른쪽으로 회전시킨다
      • RR 회전 : 왼쪽으로 회전시킨다
      • RL 회전 : 오른쪽으로 회전시킨 후 왼쪽으로 회전시킨다

회전

  • LL 회전

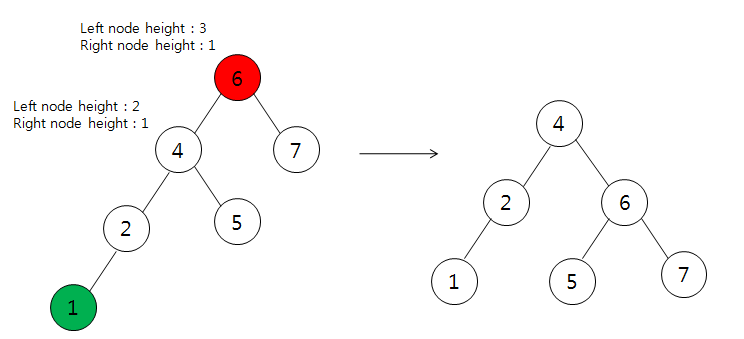
1. B <- A의 왼쪽 자식 
2. B의 오른쪽 자식을 A의 왼쪽 자식으로 만든다  
3. A를 B의 오른쪽 자식 노드로 만든다


  • RR 회전

1. B <- A의 왼쪽 자식 
2. B의 왼쪽 자식을 A의 오른쪽 자식으로 만든다  
3. A를 B의 왼쪽 자식 노드로 만든다


  • LR 회전

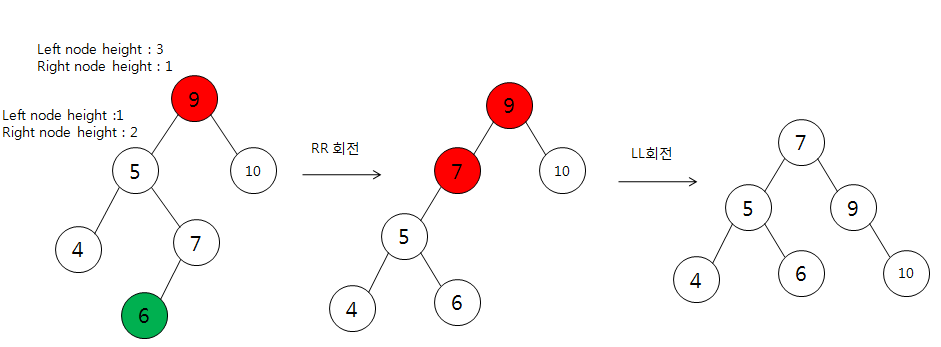
1. RR 회전  
2. LL 회전


  • RL 회전

1. LL 회전  
2. RR 회전


code


참고

  • http://girlsy7.tistory.com/134
Published 06 February 2016
DataStructure